Big important prologue note: What I wrote below is completely my original thoughts and words. In what I think is a first for the blog, I found some literature that is frankly equal parts deflating and validating. Towards the end of writing this, I came across An Algorithm to Generate Random Points in Polygon Based on Triangulation, a paper that does essentially exactly what I’m describing below. I had not heard about the paper (or any similar method) until writing about and researching this, but they did a much more formal job of explaining and justifying the idea. So shouts to Zhimin Xu, Li Zhang, and Rui Ma of Wuhan.1
Americans love arbitrary borders.2 Sure, all borders are arbitrary, but the boundary of a river, mountain range, or even road makes for a less clunky demarcation than say, a line of latitude.3 Nowhere is the art and (lack of) science of arbitrary border drawing in fuller display than US congressional districts. This isn't just about aesthetic displeasure4 - districts have stakes. The absolute least important part of gerrymandering is that the resulting shapes are hard to sample uniformly random points from. Let's talk about what makes a congressional district (shape) hard to sample uniformly from, and some ways to get around it.5
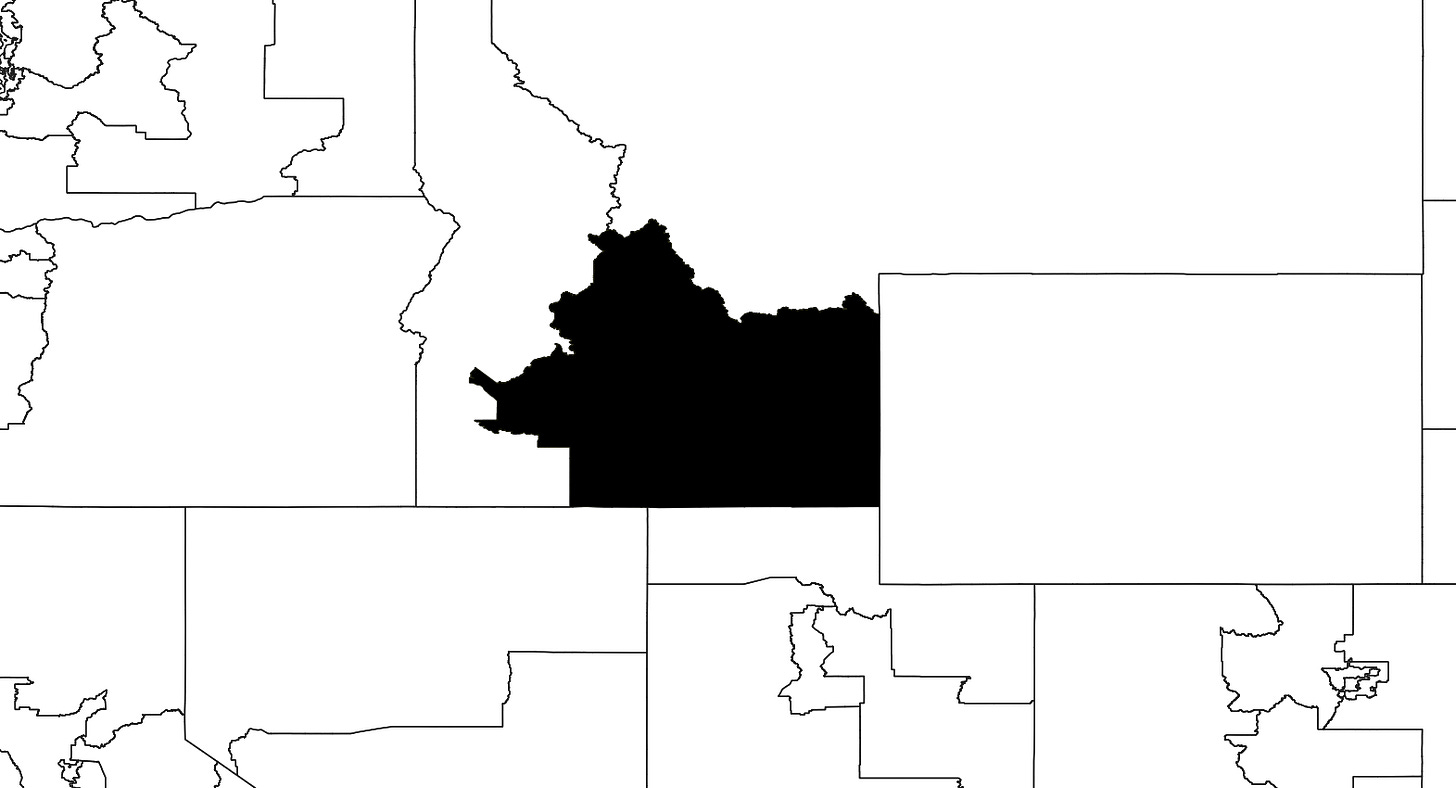
Level 1: Wyoming
A couple of easy ways to annoy a Wyomingian6 are by suggesting we abolish the Senate or by confusing their state with Colorado.7 If we have a machine that cranks out uniform random numbers (or better yet…), we can place a number along the x-axis, one along the y-axis, and be done with it. Uniformly sampling a rectangle is as easy as uniformly sampling from its span and its height. Just make sure the samples stay independent.
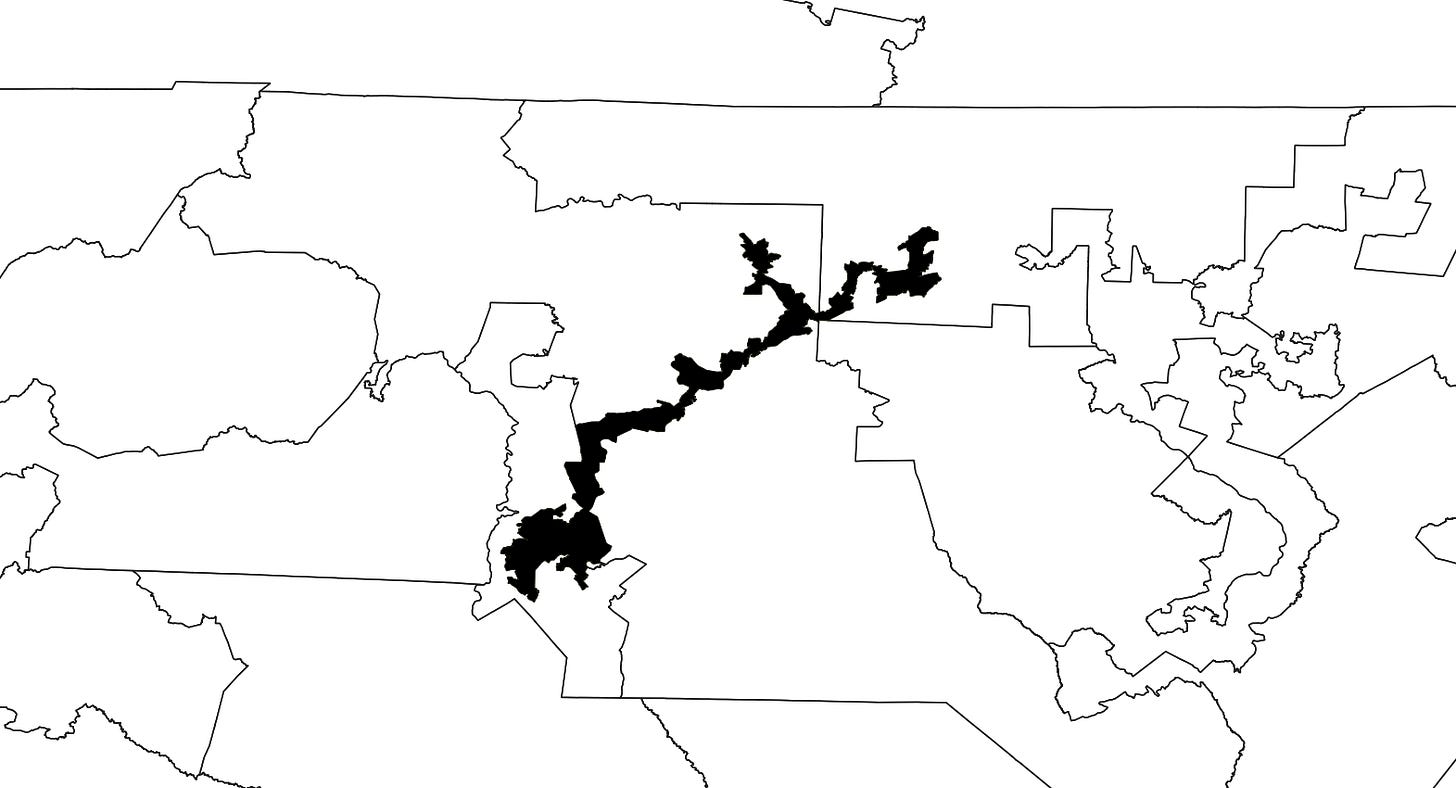
Level 2: ID-2
We don’t have a rectangle anymore, but we have something rectangle-ish,8 arguably. The common quick-and-dirty way to sample from a shape like this is to sample points from a bounding shape and then only keep the points that fall inside the shape of interest. The most straightforward choices are a bounding box/rectangle or the minimum bounding circle.9
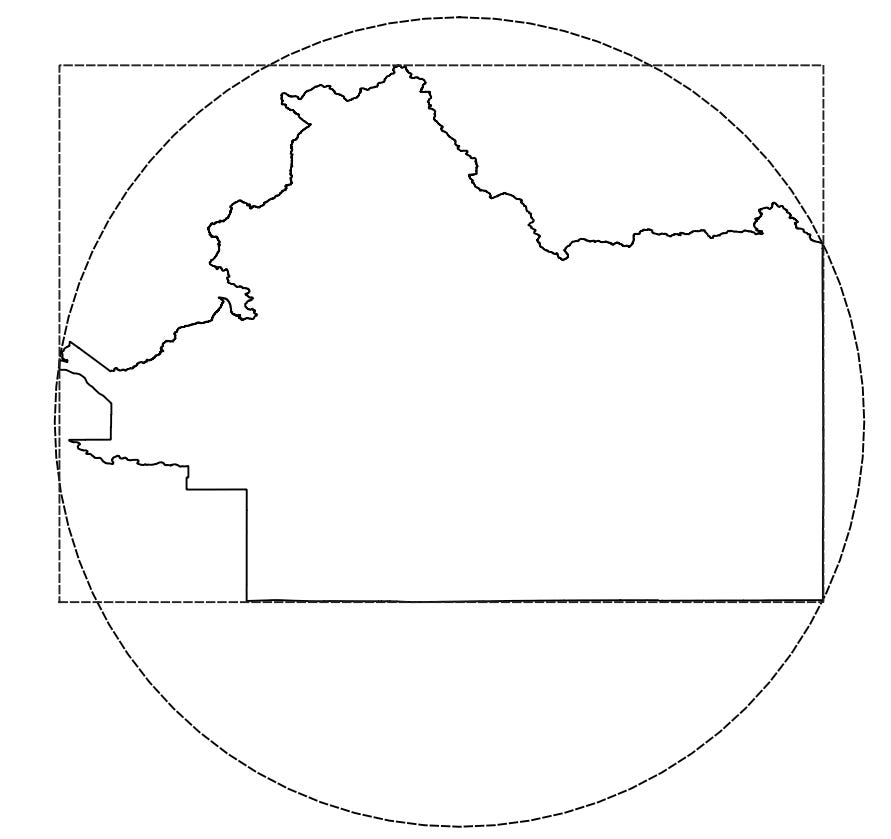
For this particular shape (and you can imagine the sort of tradeoffs that might come with other shapes), the bounding box wastes a little bit less area than the circle does. In fact, the area of ID-2 is about 51% of the area of its bounding circle and about 64% of the area of its bounding box. So if you’re comfortable throwing away over 30% of your samples, and don’t mind the added computational cost of checking each point, bounding box and filter is a great way to go. If the shape isn’t so friendly though…
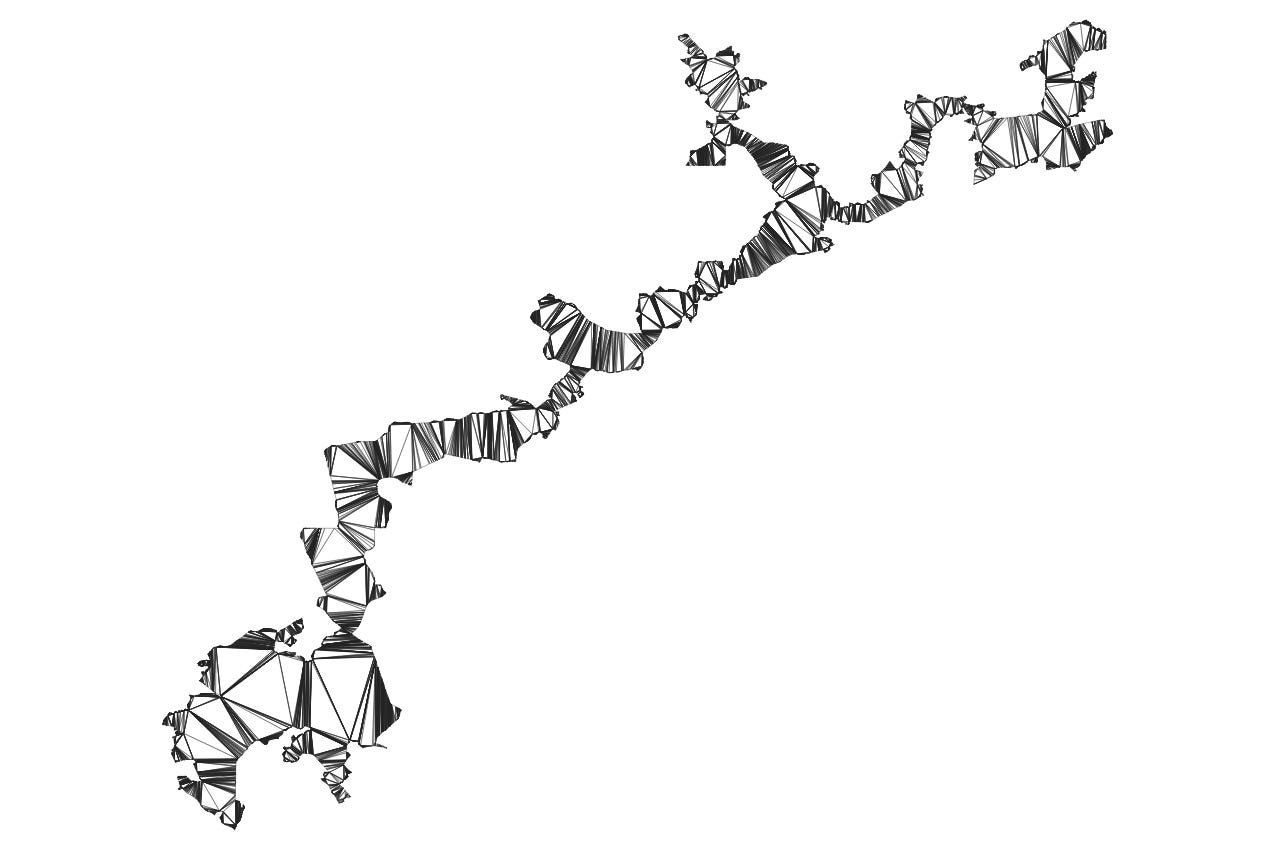
Level 99: NC-12
In fairness, this district has since been changed to a much more compact shape that better represents the population of Charlotte, North Carolina. It was a great example of gerrymandering though and therefore a wonderful case for a poorly-behaved polygon. It covered a little over 10% of the area of its bounding box10 and about 7% of its minimum bounding circle. So how do we sample from it without burning our number generating machine out ten times faster than we need to? The first step is polygon triangulation.
We cut our giant monster into a million tiny monsters, most of which in this case are very thin.11 The great part about having all of these triangles is that we know their areas, and if we want to sample uniformly from the big monster, that’s the same as sampling from the collection of little monsters in proportion to their respective areas. Luckily, someone already solved uniform sampling from an arbitrary triangle for us. We don’t have to check if the point is inside (hence “guess-free”), and we don’t have to filter any points out, saving computation time with a bit of upfront work. The lesson, as always, is proportional representation to preprocess your shapes.
The capacity for mathematics to span space and time, allowing people who never met (and in all likelihood never will) to have this point of understanding, makes me genuinely emotional. I don’t speak ancient Greek, or Babylonian, or Mandarin (or literally any other language for that matter) but I can speak math with billions of humans through history and across thousands of miles and have that small simpatico about how we see our universe. How could I not get emotional?
Could I have just said colonial powers? Absolutely. Humans in general? Arguably. I’ll just stick with making fun of my own weird nation and you, dear reader, can extrapolate and generalize as you wish.
Looking at you, New Mexico-Oklahoma border.
A few caveats. I’ll just be talking about planar polygons, so no 3d shapes, non-Euclidean surfaces, or curved edges. This isn’t exactly right since we live on a famously non-Euclidean surface, but for this purpose I effectively used the Mercator projection. We also thankfully don’t have to factor in contiguity. Extra credit reading is the wonderfully titled Shapes on a Plane.
Oof. I did not make this up I swear.
Although really that’s more of an insult to Colorado. Zing!
Very advanced jargon in use here.
Sampling from a circle uniformly is a bit less trivial (and more interesting!) than it sounds. Here’s a very well explained post about how to do this the right way.
We could be a little bit more careful here. A simple rotation would shrink this shape’s bounding box considerably, since it spans a diagonal. Not something that would meaningfully impact ID-2, because of the neat southwest corner. For those who wonder, we might choose a rotation using Principal Component Analysis. Of course, rotation doesn’t affect minimum bounding circle.
There doesn’t appear to be consensus about what to call this action. Wiki has “polygon triangulation“, which seems to get confused often with Delaunay Triangulation, and the freeware GIS tool I use (QGIS) refers to it simply as tessellation, which strikes me as unspecific.