Numeral Systems
This post has scores of dozen-word sentences.
The charge of an electron is negative. Positive spin means counter-clockwise.1 PEMDAS. We have a lot of conventions in science and mathematics, but few human conventions are as mutually widespread and arbitrary as base 10. When you read that, you heard “base ten” but if I succeed over the next few paragraphs, every time you see 10, you’ll get a mild headache remember just how many choices we had when it came to our numeral system and wonder again why it had to land here. So… why did it land here?2
Notational Frameworks
Have you ever seen a more enticing section title?
I think most of us3 are familiar with at least two notational frameworks that don’t align with decimal: tally marking (for keeping score in a game, or tracking streaming events) and additive/subtractive notation (the one used by Roman numerals).
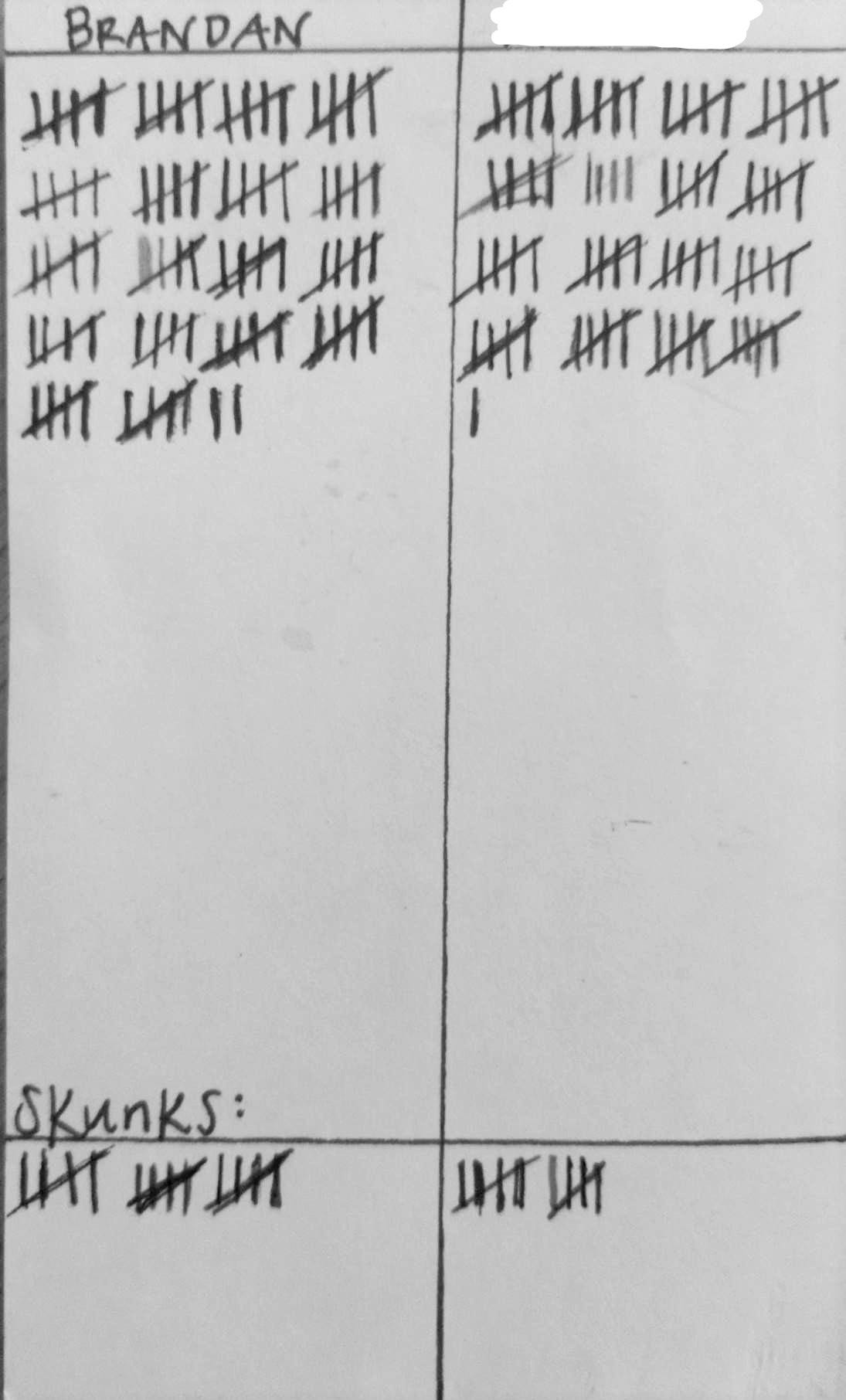
Tally marking is on its face very useful! It’s unlikely to ever go away because of its convenience in keeping track of discrete events. Counting on our fingers also does this, but that’s of course a little less permanent. In typical use, tally marks are append-only4 and effectively interchangeable with unary notation.5 Because there’s only one numeral, and every mark is added together, tally marking is both an additive notation (like Roman numerals) and a positional notation (like decimal as I’ll talk about in a bit) with the unusual base of 1. The “information density” of tally marks is the biggest drawback, as the length of the numeral representation grows linearly6 with the number itself.
Roman numerals as a system are all over the place, and I would expect any additive notation to bring with it similar confusion. The core idea is to have a different symbol for every number of a certain size. For the Romans, I is 1, V is 5, and so on.7 This solves the information density problem of tally marks. After all, we just need one marking (M) to communicate the number 1,000. One problem is when you, well, start running out of symbols.8 Another, which was never fully solved even by Romans, is the syntax and conventions around subtractive notation.9 Most modern ways of formalizing Roman numeral syntax only allow one subtractive marker10 but Latin speakers said things like duodeviginti (two from twenty) in reference to 18, so IIXX was sometimes more natural to a native speaker than XVIII.11 Words like duodeviginti (and the chosen numeral placements at 5, 10, 50, 100…) reveal the Roman tendency towards powers of 5 and 10. As justified (or not) as this tendency was, the shortcoming of this numeral scheme weren’t in its base (alone), but its structure. Tally marks have a single numeral but zero information density, while additive notation makes gains in information density by requiring (eventually) infinite numerals. Enter12 positional notation.
As the Babylonians discovered long before Latin was ever spoken, positional notation uses a finite number of numerals to represent arbitrarily large numbers with accelerating density.13 They did this with a specific sort of mixed 10/60 base that persists to this day in some places. But regardless of base this is great! A ton of information density and finite numerals means we can talk about really large numbers without taking up a ton of ink and paper or memorizing arbitrary symbols.1415 In my own early math education, positional notation was described to me as a series of “places”, as in, the “ones place, tens place, hundreds place”. Formally, positional notation sneaks in a combination of exponentiation, multiplication, and addition all in one series of ordered numerals. Take 123 as an example. There is a 1 in the hundreds place, a 2 in the tens place, and a 3 in the ones place. Each “place” is an additional power of 10 because… well because we16 picked it.
Number Bases
So you’re sold on positional notation as the best system for communicating quantities, and all that’s left now is choosing a base (or radix). What are some natural choices? Well, two is the smallest we can get while still avoiding the problems of tally marks, maybe three for its balance, four is the smallest square, we have five fingers on each hand, six is divisible by two and three (the smallest and only concurrent primes), seven is my favorite number… you see the problem. And this problem has pestered us since we as a species started talking about numbers! You can see the echoes of different bases everywhere, as long as you’re looking.
Computers of course use binary (and/or depending on how you think of it, hexadecimal), a byproduct of the most minimal way to convey information: 0/1. Imperial measurements are at least partially ternary, with three feet to a yard for example. Our clocks17 (and angles18) are base 60 because of those Babylonians, which is why your microwave thinks 123 = 83. Timekeeping is also closely linked to duodecimal, in both hourly and monthly units.
As far as anyone really knows, though, it’s not radix economy or prime divisibility or anything else that won out in the base wars. In the end, it all points back to counting on our fingers. If only we had an extra on each hand.
Grab Bag
This is just going to be a list of random number systems I find interesting. I’ll add some after this is published because I’m constantly stumbling onto new ones. Some use a specific base, some don’t,19 but I think they’re all worth mentioning if just to change the way we conceive of numbers and numerals. Send me one you find interesting!
Kaktovik Numerals
This is the splash image for this post because I love these symbols for their simplicity so much. This system is a “mixed” base, shared between 5 and 2020 and beyond 20 make use of positional notation. Kaktovik numerals are the product of a very fascinating collaboration between a class of Iñupiat students. Here’s an amazing video about doing arithmetic with these numerals.
Irrational Bases
These are numeral systems within the subset of the weird world of non-integer base numeral systems. Most common bases here are e, π, and the golden ratio φ. Sets up the wonderful pun Phinary. For all the interesting parts of these systems21, most have problems with ambiguity (representing the same number in multiple different ways). Best to leave these alone unless you’re doing some heavy duty computation.
This honestly sent me on a deep rabbit-hole, as I started writing a half-joke of a footnote about being annoyed by clockmakers. Turns out, the “clockwise” convention was handed down all the way from sundials used in the northern hemisphere. I will resist the temptation to convert a rant about watchmakers into a rant about colonialism. Although, any rant about ubiquitous arbitrary numeral systems is going there anyway.
I am Not An Expert on the history of math. It’s only a recreational interest of mine, and there have been volumes of encyclopedias dedicated to the topic. Read those! Tell me where I’m wrong! End caveat.
Dumb yankee/English only speaker caveat.
The original immutable ledger.
Unary is interesting. It’s bijective, which means “every non-negative integer can be represented in exactly one way using a finite string of digits”. Contrast this to say, decimal, where 123 is equivalent to 123.0 (or, more uncomfortably to our eyes, 0123). Chill out sigfig pedants, we’ll get to scientific notation.
I.e. in tally marking, the number n has n digits. Contrast to decimal, where for example it takes three digits to communicate the number 123. Foreshadowing!
And by “so on” I mean there is no pattern.
Or, more likely, run out of symbols that people can remember.
You could (but shouldn’t) write 19 as XVIIII (fully additive, four 1s more than 5 more than 10), XVIV (1 less than 5 more than 5 more than 10, oof), or even IXX (1 less than two 10s). Roman numerals are clearly not bijective.
e.g. IX is valid, but VIII is valid instead of IIX despite the difference in length. A difference Romans seemed to be very aware of, as the shortest representation was sometimes chosen over the “correct” one.
As a child I had no shortage of anger for clock colloquialisms like “quarter to -”. You’re telling me that in order to communicate with you effectively, I have to do subtraction in my head? Ok maybe this anger made its way out of childhood.
Enter (thing that is older than Roman numerals).
Maybe a weird phrase? All I mean is that it takes fewer and fewer digits to capture more and more numbers. I.e. for positive integers, nine numbers can be represented with a single digit, ninety are double-digit, nine hundred are triple-digit, etc.
Yes, all symbols are arbitrary, you’re very smart.
One of the earliest and most interesting uses of positional notation was in Hindu cosmology. It’s hard to talk about the age of the universe without an idea like “billions upon billions”. The Buddha himself is said to have named powers of 10 nearly up to what we now call septendecillion (10 to the 54th power).
The royal “we”.
Everything goes back to horology.
Calling angles sexagesimal is a little weird since we really use base-360 for degree trigonometry but you get the point. Shouts to Jason Kidd for turning that team around.
A lot of them are going to be from dead languages or native peoples that have since been subsumed by decimal. Colonization robs us all.
Like the Mayans!