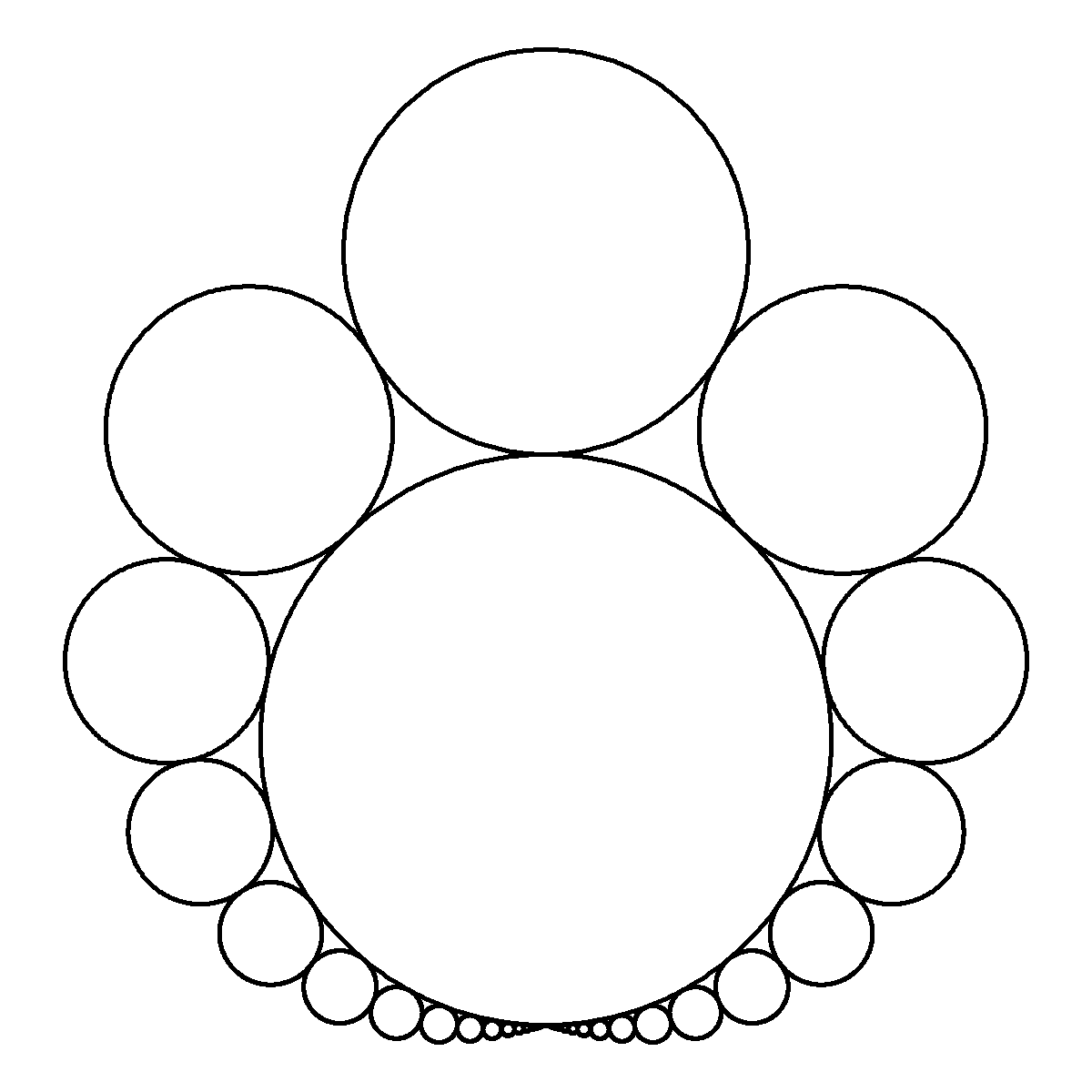
It is a dark day here at achromath. After a thorough and painful editorial review1, we have uncovered our publication’s first big mathematical error.2 The person responsible (me) was promptly fired, but a contractor with extremely relevant experience in the field (also me) has been hired as interim President and Chief Mathematical Officer. I hope I can rebuild trust where my predecessor left the charred remains of connected shrinking circles in your heart, dear reader.
I’m of course speaking about Convergent Chain Curling. Even at the time of publication, I made a note of my uncertainty around the wedge point between the first and second circle. I said this:
I don’t know if this would ever touch the second link and ruin the convergence despite its rapidly decaying angle, but that proof is probably beyond me.
Apparently not!3 Now, I’m certain that this touch-avoidance constraint is a stricter (and therefore necessary) way to frame the problem than the angular one I used. Using the elusive (but ultimately wrong) decay factor of 0.82393… I found the damning re-anchor at circle 23.45
Welp, let’s jump back in.
I’m Not Touching You
How do we do this the right way, then? We directly make the definition (absence of re-anchoring) the constraint. It’s a little goofier to read, and there are some initial conditions that we have to push the actual binary search through6, but it’s doable.7
What I found right away when I ran this was this wonderful curve that (at the right hand limit) approaches the very same decay factor we found the first time around. It also shows how (starting at circle 29) the maximum decay factor for a given circle is too big for the circle(s) before it. In other words, if I find the sweet spot that makes the 500th circle tangent to the second, the 499th is going to have overlapped already.

This feels kind of unintuitive8, but this means our constraint for this infinite set isn’t the infinitieth9 circle. It’s the 29th. The bubbles are not smooth, and the chain doesn’t go all the way around the first circle because one of these lumps is a stricter constraint than the angular one. So the curve butts up against the second circle and then retreats back away. That’s fine10, and this is what it looks like. For the record, our new maximal decay factor is about 0.82296, below our old benchmark by less than 0.001. But now circle 29 is nice and snug.
I Know You Are But What Am I?
In the spirit of some very early achromath content (making geometry-adjacent stuff just because it looks cool), and because I was curious whether I could back into a problem that made use of the angular constraint, I present the split chain11:
The setup of the problem was almost identical to the original infinite sum of angles, but with half the terminal angle (and I do it twice). Work un-wasted. Might make for a cool tattoo.12 For those of you who care, this decay factor comes out to about 0.7092776.
Am Not Times Infinity
I closed the original Convergent Chain Curling post with a few ideas about where else you could explore this geometric space, and those are all still interesting, but I have one more that I haven’t been able to shake out of my head. It tastes like a sinister puzzle but has the comfort only integers can offer in a space otherwise full of irrationals.
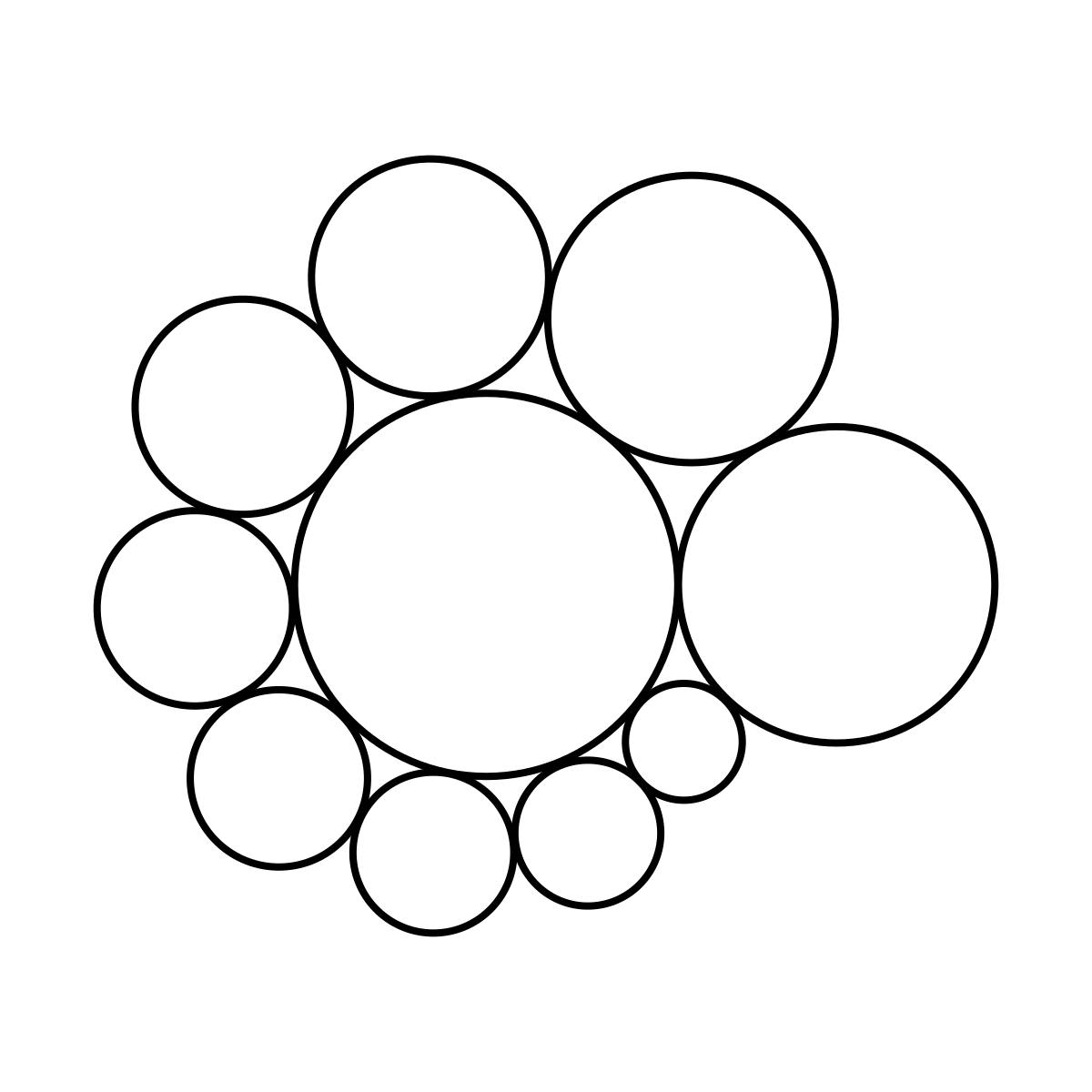
The prompt is this: Can we find a set of decreasing13 integer radii that make one full revolution around the center circle perfectly? It might look something like this (if we knew each of these radii were integers).
I’ve pretty much exhausted my endurance for this problem space (for now) so I’ll leave this as an exercise for the reader.14 You certainly can’t do worse than my disgraced predecessor.
Since posting this “puzzle” on one of the last bastions of good internet stackexchange, there have been a few solutions, all with very large integers. The path to a solution is pretty incredible and (to me) not immediately intuitive. Cool math, less cool visuals.
AKA me doodling some more.
We’ve made many small ones that we don’t care about so don’t mention them.
This was an overestimation of the difficulty of the (dis)proof, not an underestimation of my genius.
23! Embarrassing really. In my defense, I checked much larger numbers and later circles tuck back under and stop intersecting. I talk more about this in the next section. In one sense this was a huge oversight, but in another it was a wrinkle that gave me an excuse to revisit this wonderful problem space.
The first handful of circles aren’t really meaningful because it takes 7 to go all the way around at a decay factor of 1 (the hexagonal tessellation).
I considered a quick summary of the math here but nobody is interested in that. The pictures are the fun part.
I write a lot about beauty in mathematics, and it’s tempting to focus only on the intuitive, patterned, predictable parts of that beauty. But beauty is sometimes surprising, chaotic, even borderline infuriating. There’s beauty in a simple question refusing to conform to a simple answer, in the absolutely unexpected.
Infinity-th? You get what I mean.
It’s FINE. Can you tell how fine I am with this outcome?
I made a bit of an aesthetic choice here, to split only after the second circle. You can split immediately but I didn’t find that math as easy graphic as pleasing..
I have infected myself and many loved ones with math tattoos and I have no intention of stopping!
They need to strictly decrease and not be equal, or we’ve got some trivial solutions immediately with the honeycomb of 7 identical circles.
More likely: me, later.