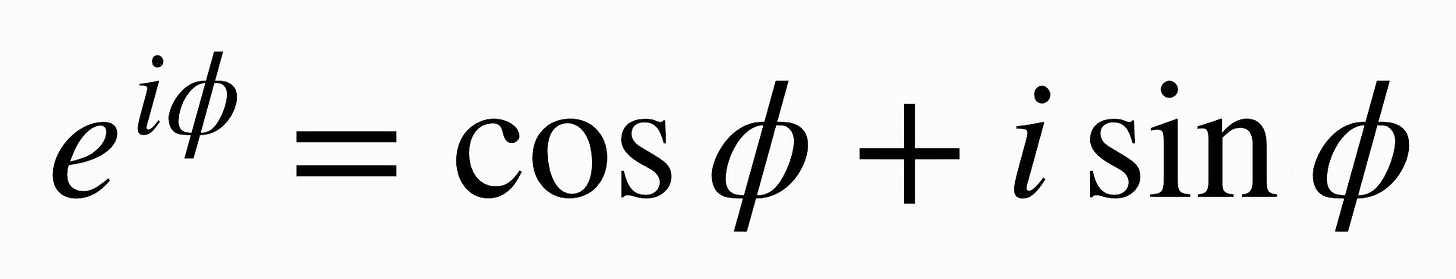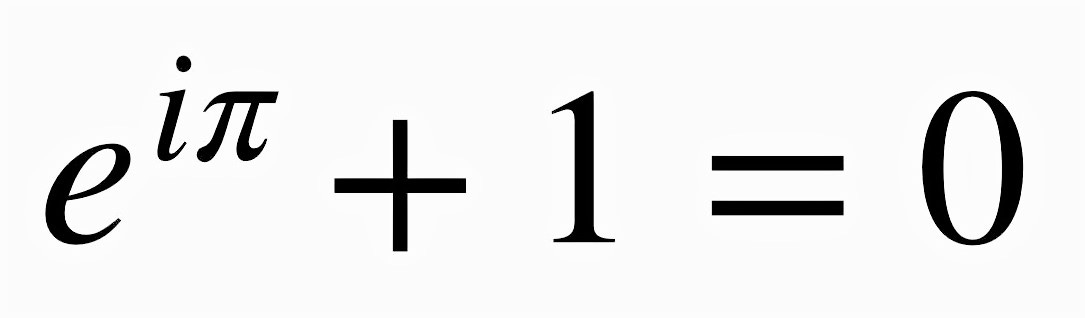Euler's Unification of Identities
Or, as it's been called in countless other places, the most beautiful equation ever discovered.
Identity is arguably1 the most fundamental idea in mathematics. To say two values (or functions, or spaces, or expressions) are identical is to say they are equal and interchangeable, even dare I say it, indiscernible. Identity helps us simplify, understand, and discover relationships between otherwise disparate mathematical ideas. It helps us sum infinite numbers of infinitesimal quantities, communicate complex relationships in familiar forms, and (when identity is disproved) reject impossible conclusions that proceed from assertions whose truth is unknown.2 Let’s talk about what it means for something to be An Identity, starting with some familiar figures and working our way out of “reality”.34
Crawling: The Arithmetic Identities
While you may never have conceived of 0 or 1 as universal constants (like we’re taught about π from the beginning), both are as critical as they are simple to understand. Addition and subtraction are the extension of perhaps the most natural human mathematical operation: counting.5 The Additive (Subtractive) Identity is whatever constant makes x+c=x (x-c=x) true for all x. For those of you who were able to do it, congratulations, and for those of you who just want to enjoy the show, it is c=0.6 So, we’re confident that 0 is the Additive Identity.7 Using similar inspection we can find and describe 1 as The Multiplicative (Divisive8) Identity.
Walking: The Trigonometric Identity
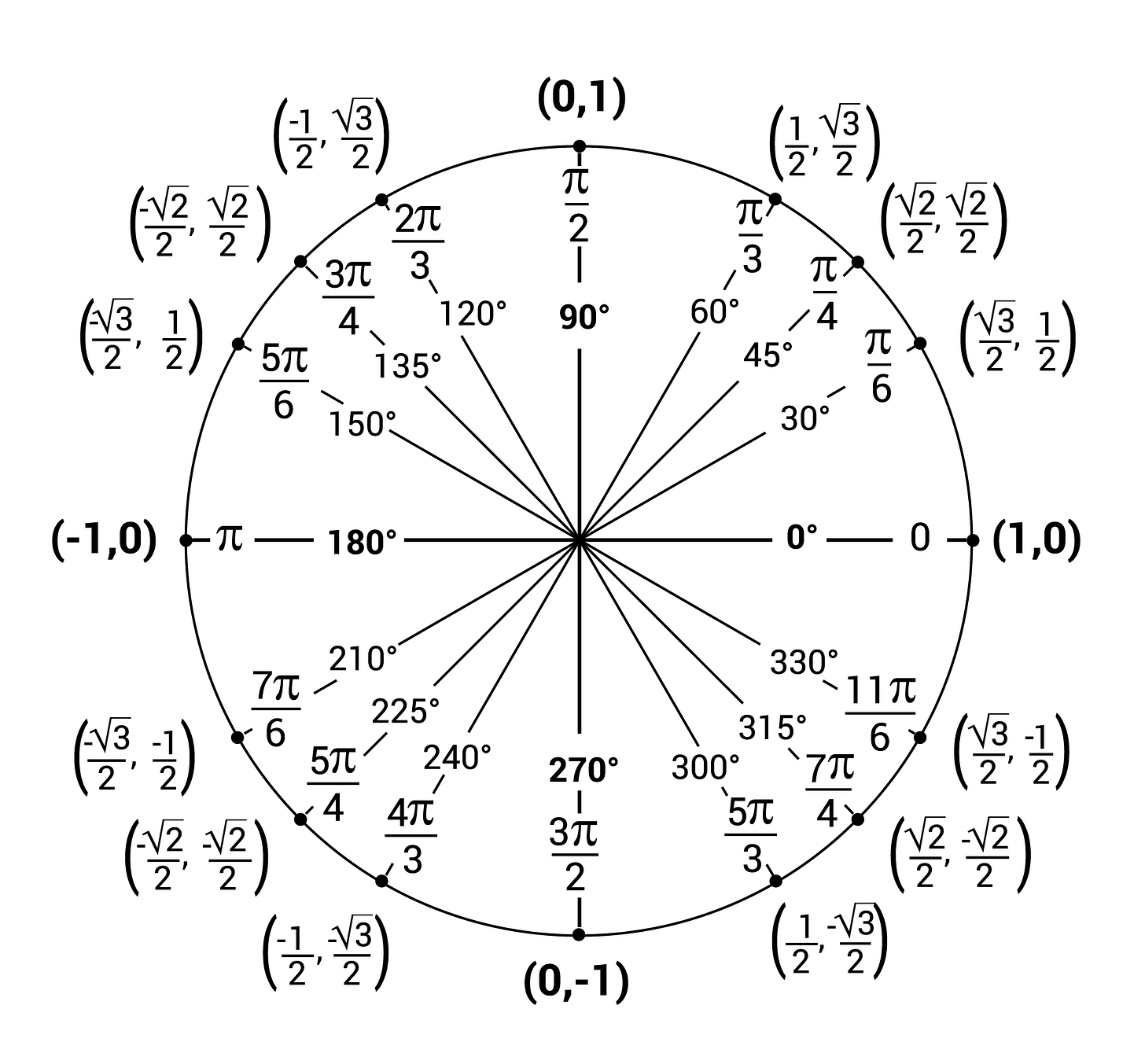
Let’s move on to more complex, non-integer constants. Take sin(x) or cos(x) or really any of the six fundamental trigonometric functions and ask what their period of repetition is. Or, said another way, when does sin(x+c)=sin(x)? The only answer that works for any x is c=2π.9 This constant π is definable and discoverable in many different ways (most commonly as the ratio between a circle’s perimeter and its diameter), some of which seem completely disconnected from others. The important parts to remember for our purposes is that it’s real, irrational, and inescapable as a fundamental piece of reality.
Running: The Exponential Identity

All roads lead to e. Continuously compounding interest, probability theory, factorials,10 calculus. If any constant has a bone to pick with the disproportionately high fame of π, it’s e. There are no fewer than six ways to define it, all converging paths from different parts of mathematics using infinite sums, continued fractions, or (spoilers) some clever trigonometry. It’s the infinite sum of all unit fractions of factorials (woof).11 e is the number that every other number is gesturing towards. Like its rival π, it is real and irrational and is close to two-something.
Astral Projecting: The Complex Identity
At this point I’ve disposed of all pretense about the term “Identity”, but stick with me. So far we’ve got four constants, all real, and split between rational and irrational. For our last constant, find your safety buddy and join me among the imaginary numbers. We define i as the square root of -1.12 That’s back to the brevity of the arithmetic identities but with some added complexity.13 I don’t have a ton more to say about i. It’s a real number but not a Real Number, and it definitely matters deeply in all sorts of fields (including fractals, one of which is pictured above). That doesn’t mean I have to like it.
The Lob: Euler’s Formula
In the wonderfully-titled Introductio in analysin infinitorum (Introduction to the Analysis of the Infinite), Euler14 examined and analyzed the anti-intuitive equality containing a seemingly random collection of functions and constants that we now know as Euler’s Formula, pictured above.15 It has many proofs, some of which are accessible even to those with a cursory understanding of calculus.16 It connects three worlds that seem otherwise disparate: trigonometry, the complex space, and logarithms/exponentiation. This is the power of imagination, or at least, imaginary numbers. Just for fun17 let’s plug in φ=π and see what falls out. The cosine term goes to -1, the sine term goes to 0 (we successfully eliminated an irrational term, always welcome), rearrange a bit, and we’re left with, well…
The Slam: Euler’s Identity
What could I say about this that hasn’t already been said? It has everything, and nothing extra. Two irrationals, two integers, and an imaginary constant all coalesce into revealing a basic truth about reality, one without convention or exception. An absolute grab-bag of concepts and constants arrange themselves into sharp, concise clarity. Our world couldn’t be any other way than this. It evades intuition at every turn but can be proved true beyond doubt. It’s enough to make someone abandon all other pursuits and dive headlong into the philosophy of mathematics.18
This is a bald, even unjustified assertion the further I interrogate it. Counting could perhaps challenge the throne? The double-niche field Philosophy of Mathematics has a lot to say about identity, equality, and epistemology, none of which I understand (let alone could speak to or summarize). As always, tell me why I’m wrong so I can be less wrong later.
This is the basis of Proof by Contradiction.
Sometimes with the words we pick, it feels like the goal is confusion. I assume there is a lively debate within the Philosophy of Math regarding the Reality of imaginary numbers and I’ve never been happier to continue being completely ignorant about something.
Regarding these section titles: An [Operation] Identity is a constant whose inclusion in the operation retains identity. Woof. It’ll be more clear in a couple sentences. I’m using this term essentially interchangeably with the more formal “Invariant”.
Here is another assertion. How do those philosophers get anywhere?
Both 0 and 1 are special for numerous other reasons, some by convention, some by pure sublimity.
Not that kind of divisive. I sort of made this term up to be honest.
We’re inching into handwavy territory for my Identity theme. What makes the choice of π better than the choice of 2π (inconsistently referred to as tau)? Looks like the real constant is six-something not three-something. The semi-answer is in a squared trig function, whose period is a single π. Squared trig functions are an important part of trigonometric identities and have some sublimity of their own.
Or should I say, factorials!
It’s really hard to talk about e without sounding circular, because so many of the paths to the destination are named for the destination, or at least reference it.
It’s even worse than this. i and -i are both roots of -1. Fear anyone who has practice doing complex analysis.
Couldn’t help myself.
Pronounced “oiler”. Not a joke, just a personal crusade.
φ here is just the variable. Replace it with x in your mind if that makes it more palatable.
Or worse, me!
This is fun right? We’re all having fun?
Almost.