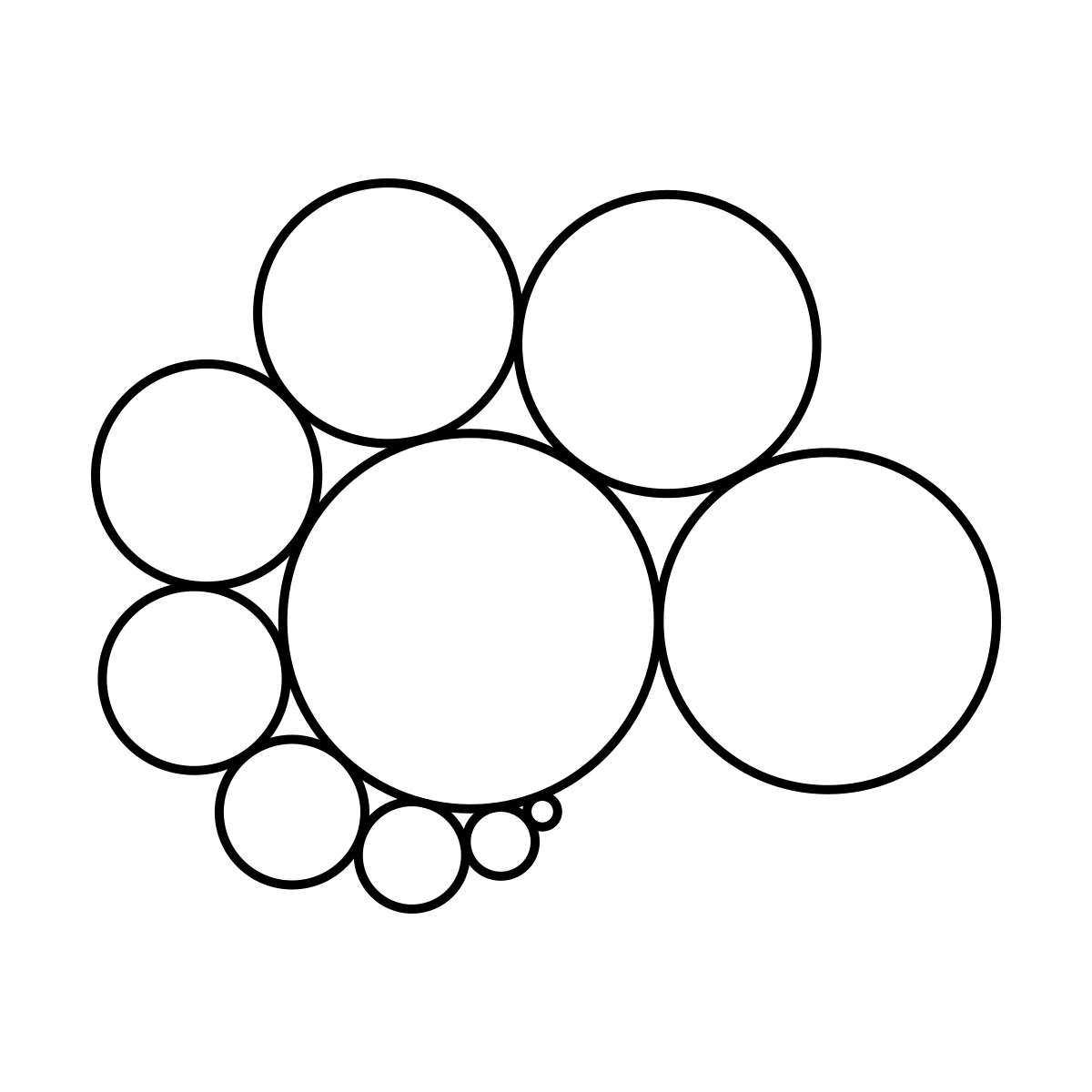
Convergent Chain Curling
Future titles will feel less like a what3words code
Note: I corrected the errors (both in method and conclusion) in this post in a follow-up here, but left those mistakes as they were at the time of publishing. Feel free to skip this and go straight to the corrected one. No extra credit for reading the prequels.
I was recently distracted1 by a geometric pattern2 in the windowsill of our midwifery.3 It was an illustration tool for cervical dilation and featured a very French-curve-reminiscent spiraling arc of cutout circles with different integer diameters.4 I saw the set of them all fitting together tangent, curled around and cuddled up like an unused bike chain. And I guess that's the lede. I want to talk about have obsessed over spiral bike chains as mathematical objects for a few weeks because I saw a cervical dilation illustration tool in our midwife's window.
Questions flooded in. What are the trivial examples? What makes a valid5 sequence of diameters? Is that chocolate or meconium on my thumb?6
As I explored these questions (and tried to coalesce that exploration into this post), I found out how many complicating factors actually exist. There are countless forks in the road of examining and describing these things, and I took the more interesting path wherever I could. I hope and plan to explore other trails later, but for now, here is my collection of thought processes and interesting findings while tinkering with these “curls”.
I found this problem space seems vaguely connected to unequal circle packing, maybe the Doyle Spiral, and another mathematical object whose name is so ridiculous I refuse to type it out. As usual, if this is already well-studied with its own 6-word name I didn’t happen to know, tell me so I can sell my computer. As will become clear, I am a recreational mathematician and my formalism is only what I would describe as 6cm dilated.7
Question 1: What do we call these?
Definitions! That’s right, we eat dessert first here at achromath.
Link: a circle of finite diameter that is tangent to the immediately previous and subsequent links8 in the chain, if they exist.9
Chain: a collection of links most directly defined by a sequence of diameters (or radii, depending on convenience).
Curl: a chain that begins at the origin and arranges links in a counter-clockwise direction tangentially.10 This is exactly what we did with the Midwife’s Curl.
We already have great bones. We can now “define” the Midwife’s Curl with a diameter sequence: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]. We also know this is fundamentally different than the same numbers in a different order. For the sake of illustration, the inverse Midwife’s Curl (going from 1 to 10) looks like this:
Right away we know a few things about curls by simply looking at them. We know transformations to the underlying diameter sequence fundamentally change the object. Inversion makes a completely new curl. The removal of a link changes a curl for all links after it (but not before!), and similarly, adding links on to the end of a curl does not require you to start again from the beginning. Every link is tangent to the links before and after it (if they exist), and another link that constrains its position. Let’s call that “other” link the…
Anchor: A link’s anchor is the latest link in the chain curl it is tangent to that is earlier in the chain than the immediately previous link.11
Each link of the Midwife’s Curl is anchored to the first link. The inverse is more interesting, though.
What was it about the Midwife’s Curl that led every link to have the same anchor? The Outhusband Curl “re-anchors” (the index of the anchor link changes) every 1-2 links, and at first glance, this appears to be driven by whether the links are increasing or decreasing in size. Could we define a curl with an infinite number of links that still never re-anchors?
Question 2: What is convergence?
Convergent: A curl is convergent if it has a terminal anchor. That is, if a curl re-anchors a finite number of times, it is convergent.
This isn’t particularly interesting for finite curls, since all of them are convergent by this definition. The obvious implication being: this is interesting for infinite curls! It’s relatively straightforward to imagine an infinite curl that converges - even one that never re-anchors. Say we start with the (trigger warning12) unit circle, and each link is 1/100th of the radius of the last, so a curl defined13 by [1, 0.01, 0.0001, …]. You would never even escape the shadow of the second link. But that’s a diameter preservation rate14 of 1/100. A rate of 1 (i.e. no decay, a curl defined by [1, 1, 1, …]), would get nowhere near converging - just the opposite - it would tesselate the plane. This begs the next question:
Question 3: What is the largest possible diameter preservation rate that never re-anchors?
And here we are, at a “… special case which contains all the germs of generality”.15 To borrow yet another quote, “The source of all good mathematics is the special case, the concrete example.”16 So, if we have a curl whose sequence starts at 1 and decays by a factor of p every link, what’s the biggest p we can have that never re-anchors? It would look something like this:

Finding this number was Not Trivial. I don’t know how watertight my approach is, but I essentially set up an infinite sum of angles, constrained the sum to 2π, and solved for p. I don’t know if this would ever touch the second link and ruin the convergence despite its rapidly decaying angle, but that proof is probably beyond me. If we focus on the aggregate asymptotic angle, the p we’re looking for is about 0.82393. Still seeking a closed form for my own mental health.
Open Ends and Unexplored Trails
Validity
There’s a whole set of curls that don’t really follow the implicit rules and assumptions I made throughout this post. Like say, [10, 10, 1, 10], which is a curl where the last element can’t be placed tangent to its predecessor. The third link is too small, and therefore buried too deep to be accessible. There are many other reasons why a curl might not “play well” but I essentially ignored all of these cases.17
Other Diameter Patterns
I did what amounts to constant multiplicative decay. The Midwife’s Curl happens to also be constant but subtractive. As you might imagine, there are any number of ways to pick how fast (or not) the diameter of links in a curl shrink (or don’t).
Alternate Definition of Convergence
Instead of the (sort of clunky) re-anchoring definition of convergence I invented, you could probably define a convergent curl to have a finite convex hull, even with infinite re-anchorings. Recall from Platonic Solids that the convex hull is the smallest convex shape18 that can contain a given shape. For example, the convex hull of the letter E19 is a taller-than-wide rectangle. Imagine you put a rubber band completely around the shape you’re considering. The shape the rubber band makes is its convex hull.
This is pure speculation and (potentially very bad) intuition, but I imagine a curl could exist that takes laps around and around, eating up half of the remaining area left in a bounding circle with each pass without ever exploding to infinite area.
Finite but Non-Zero Re-Anchoring
Even if I keep the re-anchoring definition for convergence, you could imagine a constant p for every finite number of re-anchorings. I found the constant for 0, but there are any number of those constants, depending on the number of re-anchorings you’re interested in. A generalization for another day.
Common.
Aggressively common. This particular one is up there as one of my all-time self nerd snipes, though.
And that’s as close as we’re going to get to a birth announcement here. Three footnotes in the first sentence, you poor thing.
Ten of them, to be precise. Birth is a combination miracle-nightmare.
Talk about a loaded word. I talk a little bit about this later.
One of the great unsolved mysteries.
Still lots of room to grow, too late for an epidural.
As well as others, but less predictably so, as we’ll see.
The first/last links don’t have previous/subsequent links, hence those last three words.
Perhaps the least concrete definition I use here. Maybe I’m overexplaining, maybe what I’m talking about is incoherent. Just spin the chain around the middle until it can’t move!
I know, I’m sorry. I’ve rewritten this a million times and no words are as useful as the visual.
Get it? TRIGger warning?
If “curl defined” did the same thing to your brain as it did to mine, we have the same broken brain and both need to get off youtube.
I am so bad at naming things.
From Halmos, who also has some very bad quotes like “you have to be born right” to be a mathematician.
I only entertain well-behaved mathematical objects.
I’m using “shape”, since we’re playing in 2d, but the formal definition is more generic (and much stronger!).
Same goes for HIKMNXZ, I guess depending on font.