Competition, at perhaps its most base, is a proxy for war. There are winners and losers, supporters, detractors, and neutrals. Depending on which flavor of proxy you find the most compelling, you can dive into fractal threads of news, content, hot takes, and scandal. Basketball, DOTA, chess, Ear Pull, Excel.1 Each has its superstars and its championships. Every match-up has its favorite and its underdog, and baked into every narrative and headline2 is the concept of that expected outcome. How do we form such an expectation, systematically, without just looking at the Vegas odds or trusting the talking heads?3 Turns out “we” have a lot of ways, but most of them are different flavors of Elo.
What is Elo?
If you are even vaguely within orbit of the world of chess, or familiar with the acronym MMR (Match-Making Rank for competitive online games), you are likely not hearing “Elo”4 for the first time. Elo is a system for analyzing competitor performance and predicting matchup outcomes in zero-sum games. Arpad Elo developed the system for chess5 but we can also apply it to any competition with winners and losers, like say the NBA.
Without getting into the weeds, each competitor has a rating. Higher ratings mean a better competitor, and a higher likelihood of winning. Two competitors with equal ratings have 50/50 odds of winning.6 After a game, rating is exchanged between the two competitors according to what the pre-game expectation was. An upset means the underdog takes a lot of Elo from the favorite. On the other hand, if the Globetrotters beat the Generals, they take a very small amount of Elo since we sort of already knew the Globetrotters were going to win.
A lot of the actual numerical choices are arbitrary in Elo. The starting rating, how quickly they change, how an Elo gap maps to a win probability. All just choices (and good ones considering Elo’s ubiquity!). It wasn’t the first of its kind but its clarity and predictive power took it far. In mathematics, though, you can always go more meta. Eventually, someone came along to frame Elo as a generalization of a more holistic system, and that was Mark Glickman. The way he did this was by developing a generic framework for Bayesian approximation of skill ratings, of which Elo could be considered a special (non-Bayesian) case. Before we get to the Glicko7 rating system though…
What is “Bayesian”?
This is a hard question to answer with brevity.8 A lot people who are a lot smarter than me have answered this question much better many times over, so if you’re curious, go dig around.9 The philosophy of probability is a war between two main factions: the Frequentists and the Bayesians.10
Frequentists - bless their hearts - are empirical about their beliefs about probability. “Probability” to a Frequentist is simply a re-framing of observation. What is the probability a coin lands heads? A Frequentist doesn’t know until they flip it.11 They come to the table with no opinion, for better or worse, and make no conclusions until the experiment has been repeated a few times.12
For my tone-deaf readers, I find myself convinced and compelled to throw my hat in with their sworn enemy - Bayesians. Bayesians come to the table with an opinion (they call it a prior) and constantly update it as observations are made. This opens a whole can of worms about which priors are “strong”, “informative“, or “proper”.13 Bayesians believe this can is good and worthy of opening, and that Frequentists are simply using improper priors while feigning blindness.
What is Glicko?
How does this statistical turf war apply here? The main modification that Glickman made to Elo was to transform the deviation of a rating (embedded in Elo as an arbitrary choice) into its own estimate. This is sort of an informal way to conceive of Bayesian frameworks: they turn arbitrary choices into estimates that are honed over time. Now the question is: how do we compare rating systems?
As tempting as it is to cobble together a hyper-meta zero-sum framework for evaluating zero-sum rating systems, I’ll defer to the convention here and show some ROC curves. They’re a way to capture a lot of information in a single image, but essentially do the accounting for binary outcomes and associated predictions. Better predictors have higher curves, and we can be confident that those predictors do a better job in aggregate of knowing which NBA team will win in this case.
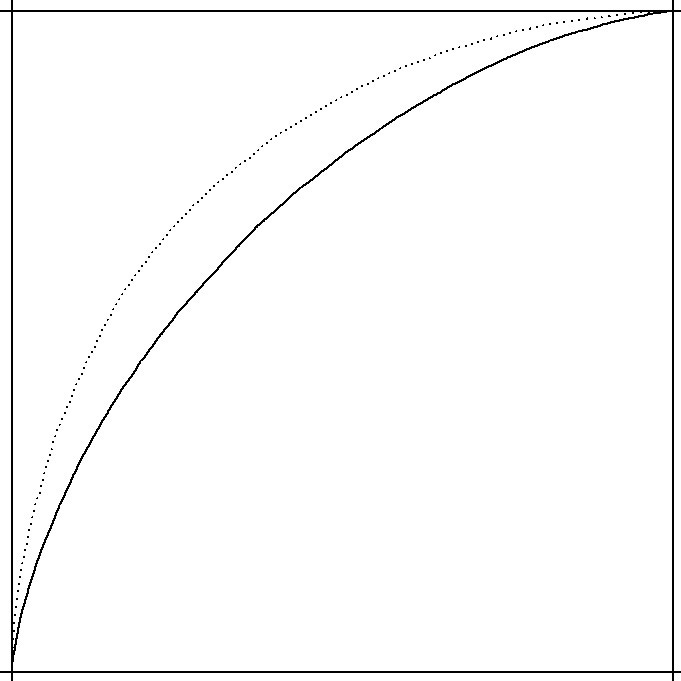
This system14 brings us to 1999. That was15 decades ago, and there are a lot of people over the years who have tried (and succeeded16) in improving over Glicko. At this juncture, though, it’s safe to say the predictive power and ease of implementing Glicko has made it a difficult standard to unseat. Just look at TF2, Splatoon, Go.
Limitations
Like any gambler17 will tell you, team ratings can't capture everything. And even if they could, unexpected things happen in sports all the time. Injuries, global pandemics, team relationships, even the confidence of individual players18 game-to-game can have huge impacts on results. No single number will ever be able to capture that much information, but at least we know how surprised to be.
Or maybe, more importantly, odds book.
Never trust the talking heads. In fact, best to just ignore them entirely.
Elo has been on a decades-long journey of de-capitalization. Is there a word for when a proper noun becomes common? Most times you see it now, it is simply “elo”, instead of the technically correct “Elo Rating”. I’ll mostly use “Elo” here to mean “Elo Rating” to stay consistent with both common usage and authorial credit.
Ironic, considering Elo has no explicit construction to handle ties besides counting it a half-win half-loss, and a draw is the most common occurrence in professional (classical) chess.
Some systems, like 538’s NBA Elo, take other things into account that make these match-ups slightly off of 50/50. Namely, the very measurable impact of home court advantage.
Yes that is the real name.
Or in general. Describing what the mechanisms of Bayesian statistics are actually doing is the work of poor, brilliant souls known as Bayesian epistemologists.
Here’s a great starting point that is very readable from outside the field: What is the Chance of an Earthquake?
What are the chances a Propensity theorist is reading this?
Enough times to fulfill the arbitrary minimum sample size.
Which begs the question, you might notice: What if the experiment isn’t repeatable? What if we’re talking about things that matter like floods or earthquakes or the day the sun doesn’t rise instead of coins?
All technical terms. Here is where I point to the sign.
Specifically, Glicko-2.
Millennial trigger warning.
I initially planned a much longer extension here, applying a relatively recent paper to the same dataset and comparing. This post was continuously delayed, and the opacity in implementing the framework became insurmountable (for a hobbyist’s dedication, at least). If you want to plug in some NBA games to the “Ingo” system, I’d be very curious to see the results.
Or bookie, or hoop-head, or critical thinker
Sorry for the stray, Ben.

